Tarefa de classificação - parte 04 | Introdução à Mineração de Dados

Redes Neurais Artificiais

Redes neurais artificiais são modelos matemáticos e computacionais inspirados no funcionamento do cérebro humano.

Inspiração biológica

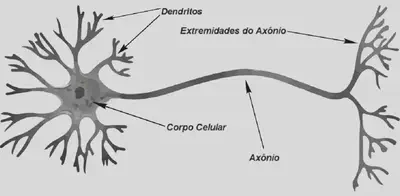
Os neurônios se comunicam através de sinapses. Sinapse é a região onde dois neurônios entram em contato e através da qual os impulsos nervosos são transmitidos entre eles

Neurônio Artificial

$$ \nu_k = \sum_{i=1}^p w_{ki}x_i +b_k$$ $$ y_k = \varphi(\nu_k)$$

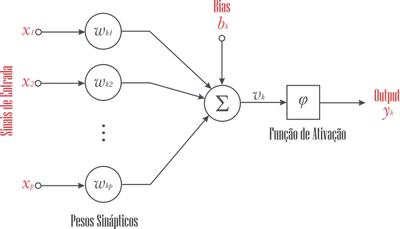
Funções de ativação

A função de ativação, denotada por $\varphi(\nu)$, define sua saída ou ativação em termos do sinal $\nu$ .

Essa função é responsável por introduzir não-linearidades nas operações realizadas pela rede neural, permitindo que ela aprenda e modele relações complexas nos dados.

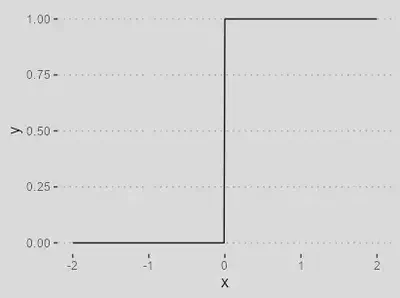
Função Threshold
`$$\varphi(\nu) = \begin{cases}1 & \text{se } \nu \geq 0, \\ 0 & \text{se }\nu < 0\end{cases}$$`

Função Threshold

`$$\varphi(\nu) = \begin{cases}1 & \text{se } \nu \geq 0, \\ 0 & \text{se }\nu < 0\end{cases}$$`

Útil em problemas onde se deseja atribuir uma saída binária, como 0 ou 1, com base em um limite.

Função sigmoidal
`$$\varphi(\nu) = \dfrac{1}{1 + \exp(-a\nu)}$$`

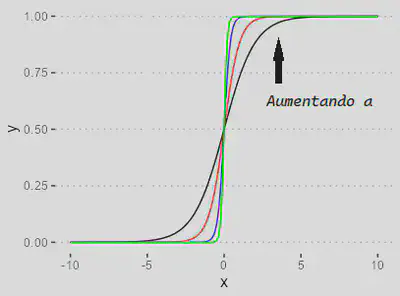
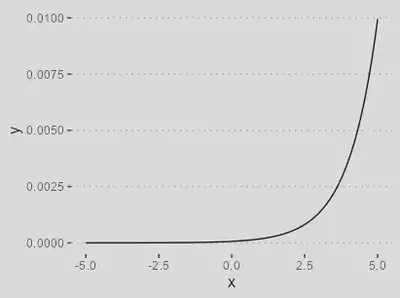
Função sigmoidal

`$$\varphi(\nu) = \dfrac{1}{1 + \exp(-a\nu)}$$`

Útil em problemas onde a saída representa a probabilidade de pertencer a uma das duas classes.

Função Sinal
`$$\varphi(\nu) = \begin{cases}1 & \text{se } \nu > 0, \\ 0 & \text{se }\nu = 0, \\ -1 & \text{se } \nu < 0 \end{cases}$$

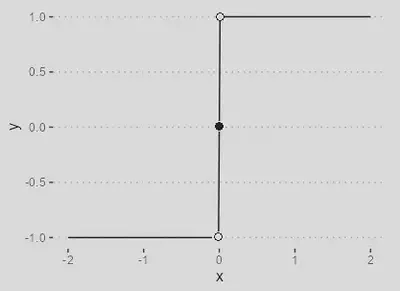
Função Sinal

`$$\varphi(\nu) = \begin{cases}1 & \text{se } \nu > 0, \\ 0 & \text{se }\nu = 0, \\ -1 & \text{se } \nu < 0 \end{cases}$$

Útil em problemas onde se deseja atribuir uma saída discreta de -1 ou 1 com base na polaridade do valor de entrada.

Função Tangente Hiperbólica
`$$\varphi(\nu) = \dfrac{1-\exp(-\beta \nu)}{1+\exp(-\beta \nu)}$$`

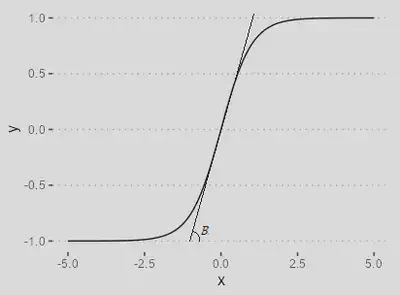
Função Tangente Hiperbólica

`$$\varphi(\nu) = \dfrac{1-\exp(-\beta \nu)}{1+\exp(-\beta \nu)}$$`

É comumente usada em redes neurais para classificação binária ou regressão.

Função ReLU
`$$\varphi(\nu) = \max(0, \nu)$$`

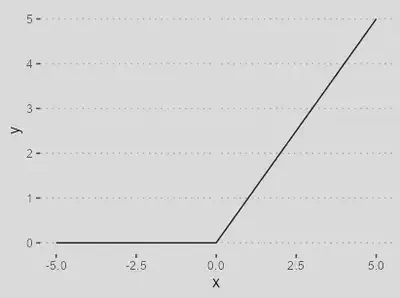
Função ReLU

`$$\varphi(\nu) = \max(0, \nu)$$`

Amplamente usada em camadas ocultas de redes neurais devido à sua simplicidade computacional

Função Softmax
`$$\varphi(\nu) = \dfrac{\exp({\nu})}{\sum_{k=1}^K \exp(\nu_k) }$$`

Função Softmax

`$$\varphi(\nu) = \dfrac{\exp({\nu})}{\sum_{k=1}^K \exp(\nu_k) }$$`

Usada para classificação multiclasse. As saídas são normalizadas, representando probabilidades.

Arquiteturas de redes

Existem várias arquiteturas de redes neurais que foram desenvolvidas ao longo dos anos para atender a diferentes necessidades e desafios.

A arquitetura de uma RNA, define a sua especialidade e qual tipo de problema poderá ser utilizada para resolvê-lo.

O que define a arquitetura de uma RNA basicamente são as camadas (camada única ou múltiplas camadas), número de neurônios em cada camada e o tipo de conexão entre os neurônios (FeedForward ou feedback)

Perceptron

O perceptron é a arquitetura mais básica de rede neural, composta por um único neurônio com conexões diretas (feedforward) de entrada e uma função de ativação.

Perceptron (1957)
	bias: ajusta a influência das entradas aprimora a flexibilidade do modelo.

Essa arquitetura é usada principalmente para problemas de classificação linearmente separáveis.

Multi-Layer Perceptron (MLP)

O MLP é uma arquitetura de rede neural feedforward com várias camadas ocultas entre a camada de entrada e a camada de saída.

Cada camada possui vários neurônios interconectados.

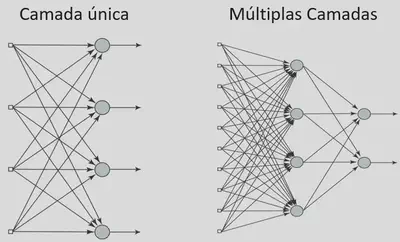
O MLP é capaz de aprender e modelar relações complexas nos dados e é amplamente usado em problemas de classificação e regressão.

Treinamento

O treinamento de redes neurais é o processo de ajustar os pesos e bias (parâmetros) da rede neural para que ela seja capaz de aprender a partir dos dados de treinamento e gerar previsões precisas para novos dados.

O treinamento envolve a minimização de uma função de custo ou perda, que mede a diferença entre as saídas previstas pela rede neural e as saídas desejadas.

Treinamento supervisionado

Treinamento do perceptron

Para cada exemplo de treinamento, o perceptron realiza uma propagação direta dos dados de entrada através da função de ativação.

O resultado da propagação direta é comparado com a saída desejada.

Se a saída do perceptron corresponder à saída desejada, nenhuma atualização nos pesos e bias é necessária e o próximo exemplo de treinamento é processado.

Se a saída do perceptron for diferente da saída desejada, os pesos e o bias são atualizados para ajustar o perceptron.

A atualização dos pesos é dada por:

$$\mathbf{w}(n+1) = \mathbf{w}(n) + \eta[\hat{y}(n)-y(n)]\mathbf{x}(n)$$

E a atualização do bias:

$$b(n+1) = b(n) + \eta y(n)$$

$\hat{y}(n)$ é a saída alvo
$y(n)$ é a saída da rede
$\eta$ é a taxa de aprendizado

A taxa de aprendizagem ( $\eta$) é um hiperparâmetro crítico no treinamento do perceptron:

Se for muito grande, pode levar a oscilações e a não convergência do algoritmo.
Se for muito pequena, o treinamento pode ser lento.

Geralmente seu valor varia de 0.1 a 1.0

Treinamento de redes mlp

O algoritmo de aprendizado da MLP é chamado backpropagation e é composto, basicamente, de duas etapas

Propagação: Recebimento dos estímulos que é aplicado aos neurônios da rede, onde seu efeito se propaga camada por camada até produzir uma saída como resposta da rede. Neste passo não há alteração nos pesos sinápticos.

A saída prevista pela rede MLP é comparada com a saída desejada usando uma função de custo. A função de custo mede o quão bem a rede MLP está performando em relação ao objetivo desejado.

Retropropagação: Após a saída, os pesos sinápticos são ajustados de acordo com a regra de correção de erro. Este sinal é propagado então para toda rede da saída para o entrada (caminho inverso), ou seja, o erro é retropropagado.

Vantagens e desvantagens

Vantagens: capacidade de aprendizado, tolerância a falhas, aplicabilidade em diversos problemas

Desvantagens: complexidade de treinamento, necessidade de grande quantidade de dados