Tarefa de Classificação
O que são problemas de classificação?
Os problemas de classificação são aqueles que envolvem a classificação de objetos ou instâncias em uma ou mais categorias pré-definidas.
-
Em problemas de classificação, o objetivo é “aprender” um modelo que possa mapear as características de um objeto para uma categoria correspondente.
-
O modelo é treinado com dados rotulados, ou seja, dados onde a categoria ou classe de cada objeto é conhecida.
-
O modelo é então usado para classificar novos objetos com base em suas características.
-
Exemplos de problemas de classificação incluem:
- Classificar e-mails como spam ou não spam.
- Classificar transações de cartão de crédito como fraudulentas ou legítimas.
- Classificar imagens de objetos como carros, animais, plantas, etc.
Problema de classificação
-
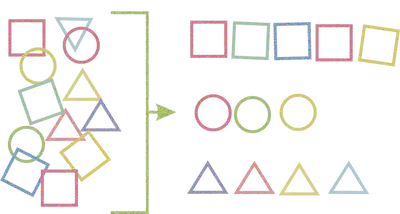
Podem ser divididos em classificação binária e classificação multiclasse
-
Em problemas de classificação binária, existem apenas duas classes possíveis (por exemplo, sim ou não).
-
Para os multiclasse, existem três ou mais classes possíveis (por exemplo, vermelho, azul ou verde).
Algoritmos de classificação
-
Algoritmos mais comuns usados para problemas de classificação:
- K-Nearest Neighbors (KNN)
- Naive Bayes
- Árvores de decisão
- Random Forests
- Máquinas de Vetores de Suporte (SVM)
- Redes Neurais Artificiais (ANN)
K-Nearest Neighbors (KNN)
O KNN é um algoritmo de aprendizado supervisionado de classificação e regressão, que usa a proximidade dos objetos para classificar novas instâncias.
É um dos algoritmos mais simples e intuitivos de aprendizado de máquina. Utiliza a ideia do “vizinho mais próximo”, o que significa que ele determina a classe de uma instância com base nas classes de seus vizinhos mais próximos.
Em outras palavras, se a maioria dos vizinhos mais próximos de uma instância pertence a uma classe específica, então a instância também é classificada como pertencente a essa classe.
Algoritmo KNN
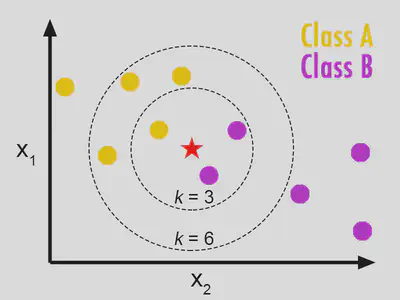
O valor de K é um parâmetro importante em KNN. Ele determina o número de vizinhos mais próximos que são usados para classificar uma nova instância.
Um valor de K pequeno pode levar a um modelo muito sensível ao ruído nos dados, enquanto um valor grande de K pode levar a uma perda de detalhes importantes nos dados.
A escolha do valor K ideal é frequentemente realizada por meio de técnicas de validação cruzada.
-
KNN é usado para problemas de classificação e regressão.
-
Em problemas de classificação, a classe mais comum entre os K vizinhos mais próximos é escolhida como a classe da nova instância.
-
Em problemas de regressão, a média ou mediana dos valores alvo dos K vizinhos mais próximos é escolhida como o valor alvo da nova instância.
-
É computacionalmente caro para grandes conjuntos de dados, pois ele precisa calcular a distância entre a nova instância e todos os pontos de dados no conjunto de treinamento.
Além disso, o KNN é sensível à escala dos dados, portanto, a normalização dos dados é importante antes de aplicar o algoritmo.
Finalmente, o KNN pode ser usado como um modelo de referência para problemas de classificação e regressão antes de explorar modelos mais complexos.
Exemplo
Compra de um computador
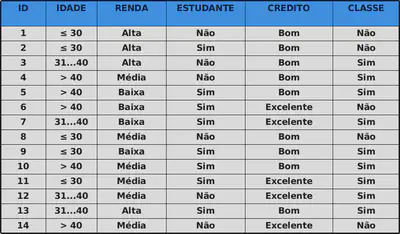
João possui as seguintes características
- menos de 30 anos
- renda média
- é estudante
- possuí um bom crédito na praça!
João compraria ou não compraria o computador?

Quem é o João?
$x_0 = (\leq 30, \text{ Média}, \text{ Sim}, \text{ Bom})$
Usando o classificador KNN com k = 5
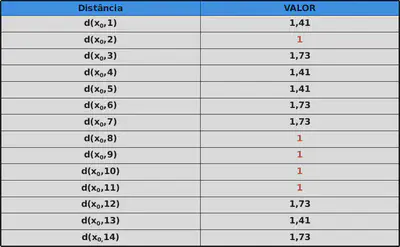
Temos então que os 5 vizinhos mais próximos a João são
-
$ x_2 = \{\leq 30, \text{ Alta}, \text{ Sim}, \text{ Bom}\}$
-
$ x_8 = \{\leq 30, \text{Média}, \text{ Não}, \text{ Bom}\}$
-
$ x_9 = \{\leq 30, \text{ Baixa}, \text{ Sim}, \text{ Bom}\}$
-
$ x_{10} = \{> 40, \text{ Média}, \text{ Sim}, \text{ Excelente}\}$
-
$ x_{11} = \{\leq 30, \text{ Média}, \text{ Sim}, \text{ Excelente}\}$
João comprará o computador?
De acordo com o KNN: SIM!
Classificador Naïve Bayes
Baseia-se no Teorema de Bayes, que afirma que a probabilidade de um evento ocorrer dado que outro evento já ocorreu é proporcional à probabilidade deste último evento ocorrer dado o primeiro.
-
Este método estima a probabilidade de cada classe (categoria) dada as características dos dados.
-
Ele assume que as características são independentes entre si, ou seja, não há interdependência entre elas.
-
Com base nessa probabilidade, ele classifica novos dados em uma das categorias pré-definidas.
Vantagens
-
O Classificador Naïve Bayes é um algoritmo simples e rápido.
-
Funciona bem em conjuntos de dados com muitas características e com pouco dados.
-
É um algoritmo eficiente em tarefas de classificação de texto.
Desvantagens
-
Assume que as características são independentes entre si, o que nem sempre é verdade.
-
Ele pode ser afetado por dados faltantes ou incorretos.
-
Não é um bom algoritmo para tarefas que envolvem classes dependentes.
Exemplo
Compra de um computador

Voltando ao Joãozinho…
$x_0 = (\leq 30, \text{ Média}, \text{ Sim}, \text{ Bom})$
Probabilidade de ocorrência das classes

$x_0 = (\leq 30, \text{ Média}, \text{ Sim}, \text{ Bom})$

Para o atributo Idade
$$ P(\text{Idade} \leq 30 | \text{classe = Sim}) = \dfrac{2}{9} \\ P(\text{Idade} \leq 30 | \text{classe = Não}) = \dfrac{3}{5}$$
$x_0 = (\leq 30, \text{ Média}, \text{ Sim}, \text{ Bom})$

Para o atributo Renda
$$ P(\text{Renda = Média} | \text{classe = Sim}) = \dfrac{4}{9} \\ P(\text{Renda = Média} | \text{classe = Não}) = \dfrac{2}{5}$$
$x_0 = (\leq 30, \text{ Média}, \text{ Sim}, \text{ Bom})$

Para o atributo Estudante
$$ P(\text{Estudante = Sim} | \text{classe = Sim}) = \dfrac{6}{9} \\ P(\text{Estudante = Sim} | \text{classe = Não}) = \dfrac{1}{5}$$
$x_0 = (\leq 30, \text{ Média}, \text{ Sim}, \text{ Bom})$

Para o atributo Crédito
$$ P(\text{Crédito = Bom} | \text{classe = Sim}) = \dfrac{6}{9} \\ P(\text{Crédito = Bom} | \text{classe = Não}) = \dfrac{2}{5}$$Temos então, sob independência:
`$$P(x_0|\text{Sim}) = P(\leq 30 \cap \text{Média} \cap \text{Sim} \cap \text{Bom}|\text{Sim} ) \\ = \dfrac{2}{9} \times \dfrac{4}{9}\times \dfrac{6}{9}\times \dfrac{6}{9} = \dfrac{32}{729} = 0,044\\$$`Temos então, sob independência:
`$$P(x_0|\text{Não}) = P(\leq 30 \cap \text{Média} \cap \text{Sim} \cap \text{Bom}|\text{Não} ) \\ = \dfrac{3}{5} \times \dfrac{2}{5}\times \dfrac{1}{5}\times \dfrac{2}{5} = \dfrac{12}{625} = 0,019\\$$`Pelo Teorema da Probabilidade Total:
`$$P(x_0) = P(x_0|\text{classe = Sim}) \times P(\text{classe = Sim}) + \\ P(x_0|\text{classe = Não}) \times P(\text{classe = Não}) \\ = 0,044 \times 0,643 + 0,019 \times 0,357 = 0,035\\$$`Assim, pelo Teorema de Bayes:
$$P(\text{Sim}|x_0) = \dfrac{P(x_0|\text{classe = Sim}) \times P(\text{classe = Sim})}{P(x_0)} \\ = \dfrac{0,044 \times 0,643}{0,035} = 0,80 \\ $$Assim, pelo Teorema de Bayes:
$$P(\text{Não}|x_0) = \dfrac{P(x_0|\text{classe = Não}) \times P(\text{classe = Não})}{P(x_0)} \\ = \dfrac{0,019 \times 0,357}{0,035} = 0,20 \\ $$João comprará o computador?
De acordo com o Naïve Bayes: SIM!