Transformação de dados
-
As bases de dados brutas e integradas a partir de bases distintas podem sofrer, além de valores ausentes, ruídos e inconsistências, de dados não ou pouco padronizados.
- Por exemplo, pode haver valores de um mesmo atributo escritos em maiúsculo e outros em minúsculo, e os formatos e as unidades podem ser diferentes.
-
Outro tipo de problema encontrado é a não uniformidade dos atributos, ou seja, alguns atributos podem ser numéricos, outros categóricos, e os domínios de cada atributo podem ser muito diferentes.
-
Como podemos resolver esses problemas?
-
Padronização: Resolver as diferenças de unidades e escalas dos dados.
- Capitalização: é usual padronizar as fontes, normalmente para maiúsculo.
- Padronização de formatos: observar e padronizar o formato de cada atributo da base, principalmente quando diferentes bases precisam ser integradas.
-
Conversão de unidades: todos os dados devem ser convertidos e padronizados em uma mesma unidade de medida.
-
Normalização: tornar os dados mais apropriados à aplicação de algum algoritmo de mineração.
Tipos de normalização
- Normalização Max-Min: Realiza uma transformação linear nos dados originais
$$X' = \dfrac{X - \min(X)}{\max(X) - \min(X)}$$
- Normalização pelo escore-z: Útil quando os valores máximo e mínimo de um atributo forem desconhecidos ou quando existe outliers.
$$X' = \dfrac{X - \bar{X}}{s_X}$$
- Normalização pelo escalonamento decimal: Move a casa decimal de um atributo
\(X\).
$$X' = \dfrac{X}{10^j}$$
em que \(j\) é o menor inteiro tal que \(\max(|X'|)< 1\).
- Normalização pela distância interquartilica: Toma o valor do atributo, subtrai a mediana e divide pela distância interquartílica ($DIQ = Q_3 - Q_1$)
$$X' = \dfrac{X - Q_2}{DIQ}$$
Exemplo de uso das diferentes normalizações
| ID | Valor original | Max-Min | Escore-z | Escalonamento decimal | Distância interquartílica |
|---|---|---|---|---|---|
| 1 | 67 | 0,85 | 0,73 | 0,67 | 0,40 |
| 2 | 43 | 0,33 | -0,92 | 0,43 | -0,80 |
| 3 | 58 | 0,65 | 0,11 | 0,58 | -0,05 |
| 4 | 28 | 0,00 | -1,96 | 0,28 | -1,55 |
| 5 | 74 | 1,00 | 1,21 | 0,74 | 0,75 |
| 6 | 65 | 0,80 | 0,59 | 0,65 | 0,30 |
| 7 | 70 | 0,91 | 0,94 | 0,70 | 0,55 |
| 8 | 42 | 0,30 | -0,99 | 0,42 | -0,85 |
| 9 | 57 | 0,63 | 0,04 | 0,57 | -0,10 |
| 10 | 60 | 0,70 | 0,25 | 0,60 | 0,05 |
- Transformação logarítmica: Usada para reduzir a assimetria e a variância dos dados. É especialmente útil quando os dados estão distribuídos de forma exponencial ou quando há um grande intervalo de valores entre as observações.
- Transformação de raiz quadrada: Similar à transformação logarítmica, com o benefício de manter a escala original dos dados, facilitando a interpretação.
- A transformação logarítmica é mais adequada para dados com caudas longas e uma grande variação, enquanto a transformação da raiz quadrada é mais adequada para dados com uma variação moderada. Além disso, a o uso de logarítmos tem o efeito de estabilizar a variância dos dados, enquanto a o uso da raiz quadrada tem o efeito de reduzir a variância dos dados.
Discretização de dados
-
Discretização é o processo de transformar uma variável contínua em uma variável categórica ou discreta.
-
É útil quando se deseja agrupar valores contínuos em categorias ou intervalos para simplificar a análise ou reduzir o efeito de valores extremos.
-
Algumas das técnicas comuns de discretização incluem:
- Discretização equi-probabilística: Essa técnica envolve a divisão dos dados em intervalos de tamanho igual, de modo que cada intervalo contenha aproximadamente a mesma quantidade de observações.
- Discretização equi-distante: Nessa técnica, os dados são divididos em intervalos de tamanho igual, com base em uma distância predefinida.
- Discretização por quartis: Os dados são divididos em quartis, com base nos valores de corte que dividem os dados em quatro partes iguais.
- Discretização por frequência: Os dados são divididos em intervalos com base na frequência de observações em cada intervalo.
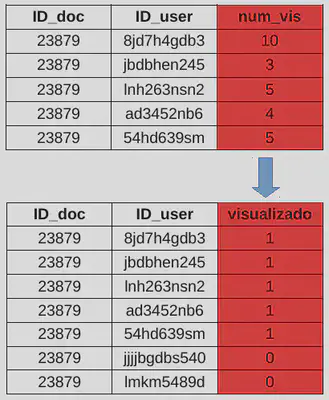
- Binarização: A binarização é uma técnica de transformação de dados que converte valores quantitativos em valores binários (0 ou 1) com base em um valor de corte.
Exemplo de binarização
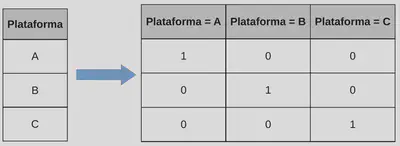
- One-Hot Encoding: O One-Hot Encoding é uma técnica de transformação de dados que converte variáveis categóricas em vetores binários para permitir a análise em modelos de machine learning.
Exemplo de one-hot enconding