Transformações de variáveis: o que são e quando usá-las na análise de dados

Olá pessoal, beleza?

Hoje vamos falar sobre um conceito muito importante no contexto de análise de dados: as transformações!

As transformações de variáveis são técnicas amplamente utilizadas na estatística e em outras áreas das ciências, como a economia, a psicologia e a medicina, além de ajudar na obtenção de modelos preditivos mais precisos. Neste post, vamos discutir o que são transformações de variáveis, quando elas são usadas e quais são as principais técnicas de transformação.

O que são transformações de variáveis?

As transformações de variáveis envolvem um conjunto de métodos utilizados para alterar a distribuição dos dados, a fim de torná-los mais adequados para uma análise específica. Isso envolve aplicar uma função matemática aos dados originais, em uma ou mais variáveis dentro do conjunto de dados, com a finalidade de normalizar a distribuição dos dados, reduzir a variância, linearizar relações ou tornar a relação entre variáveis mais clara.

Principais técnicas de transformação

Transformação logarítmica

A transformação logarítmica é uma técnica que é amplamente utilizada em situações em que a variável tem uma distribuição assimétrica e/ou uma grande variância.

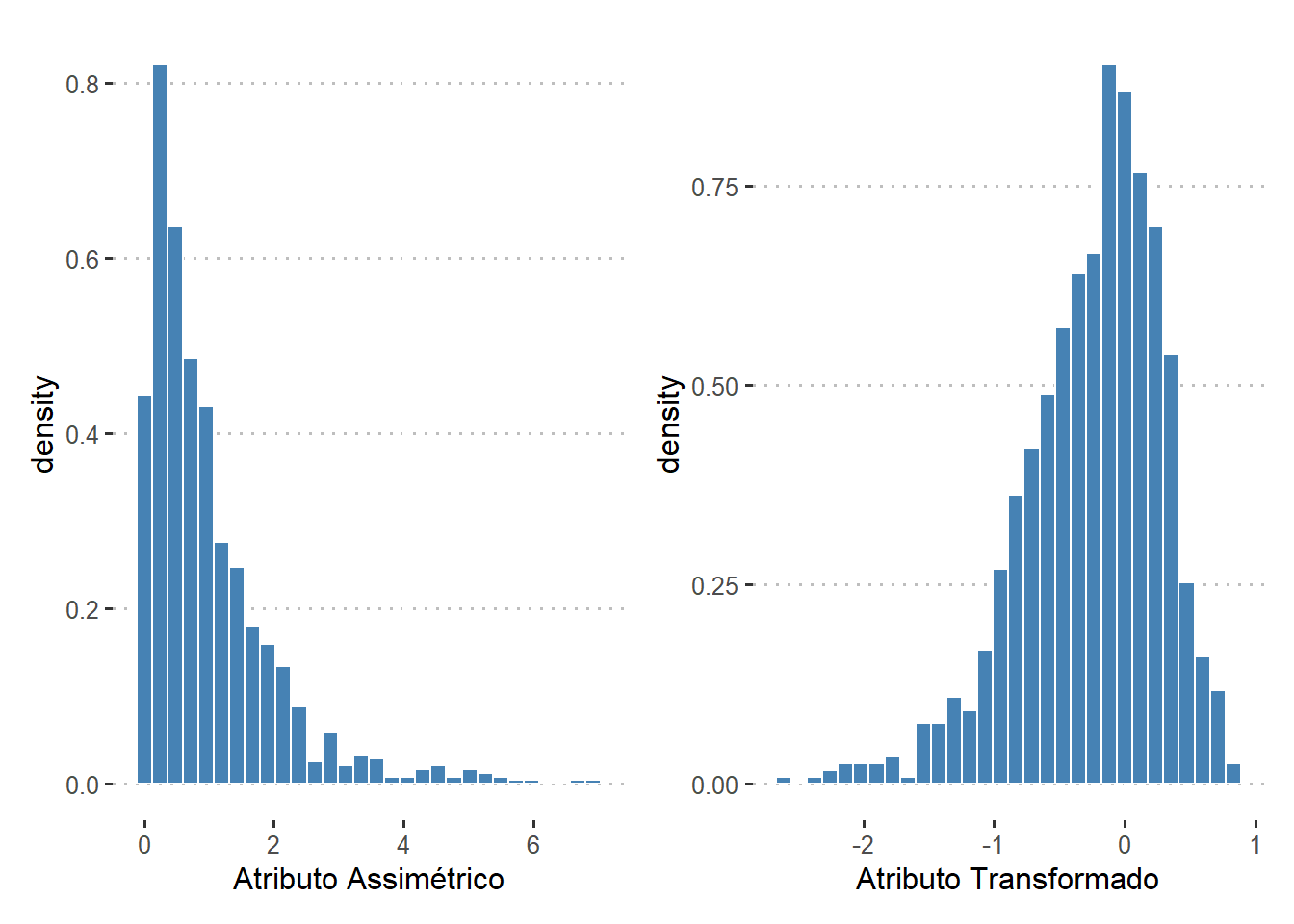
A transformação logarítmica é definida pela seguinte equação:

$$ y = \log(x) $$

onde $x$ é a variável a ser transformada e $y$ é a variável transformada. A transformação logarítmica é uma transformação monotônica, o que significa que não afeta a ordem dos dados. Isso é importante para modelos preditivos porque garante que a transformação não afete a capacidade do modelo de capturar a relação entre as variáveis.

Transformação raiz quadrada

Assim como a transformação logarítmica, a transformação de raiz quadrada é uma transformação matemática simples e não paramétrica que pode ser facilmente aplicada em modelos preditivos.

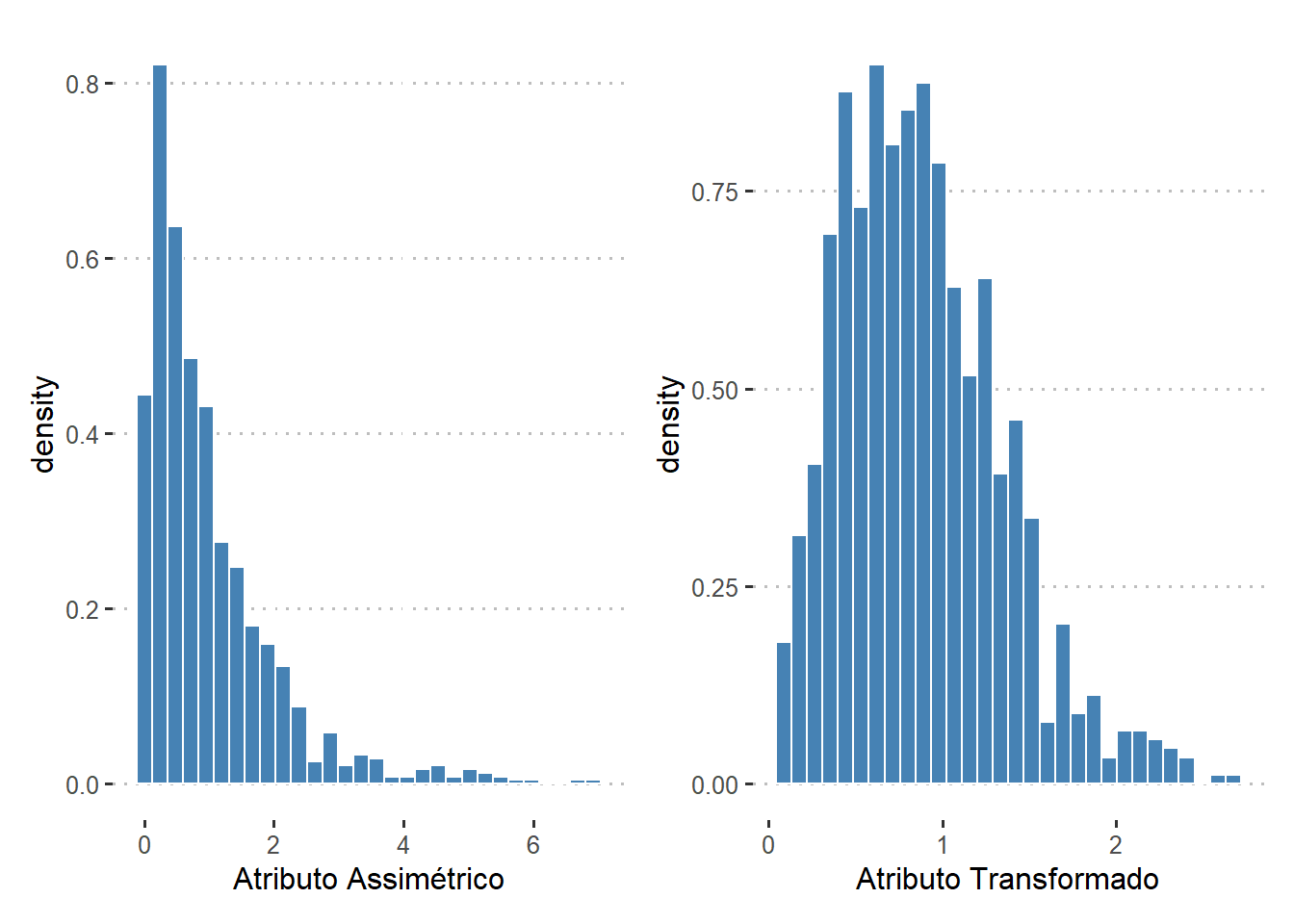
A transformação de raiz quadrada é definida pela seguinte equação:

$$ y = \sqrt x $$

onde $x$ é a variável a ser transformada e $y$ é a variável transformada. Assim como a transformação logarítimica, a transformação de raiz quadrada é uma transformação monotônica, o que significa que não afeta a ordem dos dados.

Transformação de Box-Cox

A transformação de Box-Cox é uma técnica para transformar variáveis em modelos preditivos que é amplamente utilizada para melhorar a qualidade da modelagem e a precisão das previsões. É uma técnica paramétrica que depende de um parâmetro lambda que é estimado a partir dos dados, podendo ser usada apenas com variáveis não negativas..

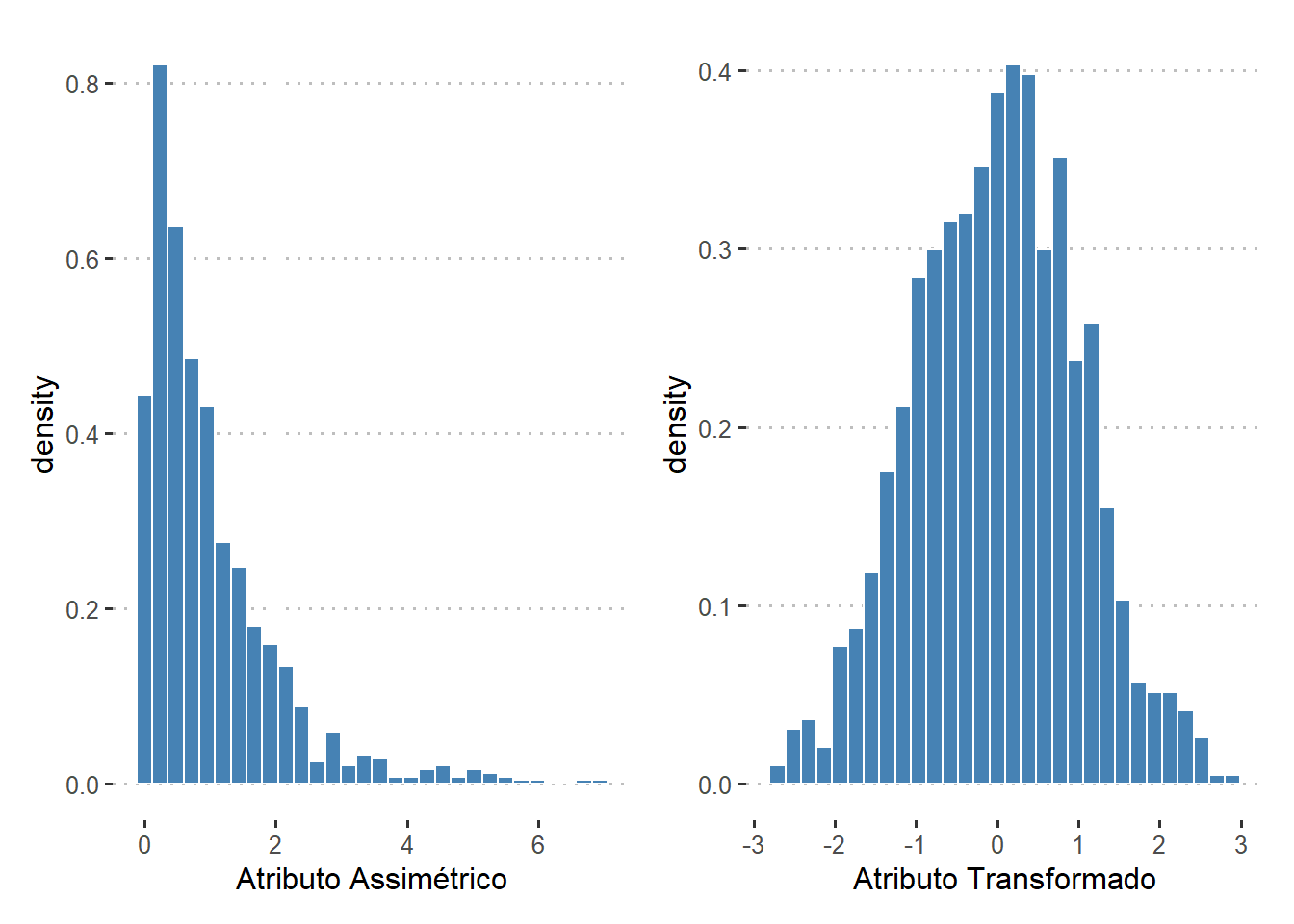
A transformação de Box-Cox é definida pela seguinte equação:

$$ y = \begin{cases} \dfrac{(x^\lambda - 1)}{\lambda}, & se \ \lambda \neq 0 \\ \log(x), & se \ \lambda = 0 \end{cases} $$

onde $x$ é a variável a ser transformada e $y$ é a variável transformada. Esta é uma técnica de transformação de dados útil usada para estabilizar a variância, tornar os dados mais semelhantes à distribuição normal, por exemplo, quando um atributo tem a aparência de uma curva normal mas está descolado para a direita ou esquerda, melhorar a validade das medidas de associação e para outros procedimentos de estabilização de dados.

Transformação Yeo-Johnson

A transformação Yeo-Johnson é uma técnica de transformação semelhante à transformação de Box-Cox. No entanto, a transformação Yeo-Johnson é mais flexível porque pode ser usada para variáveis que podem assumir valores negativos.

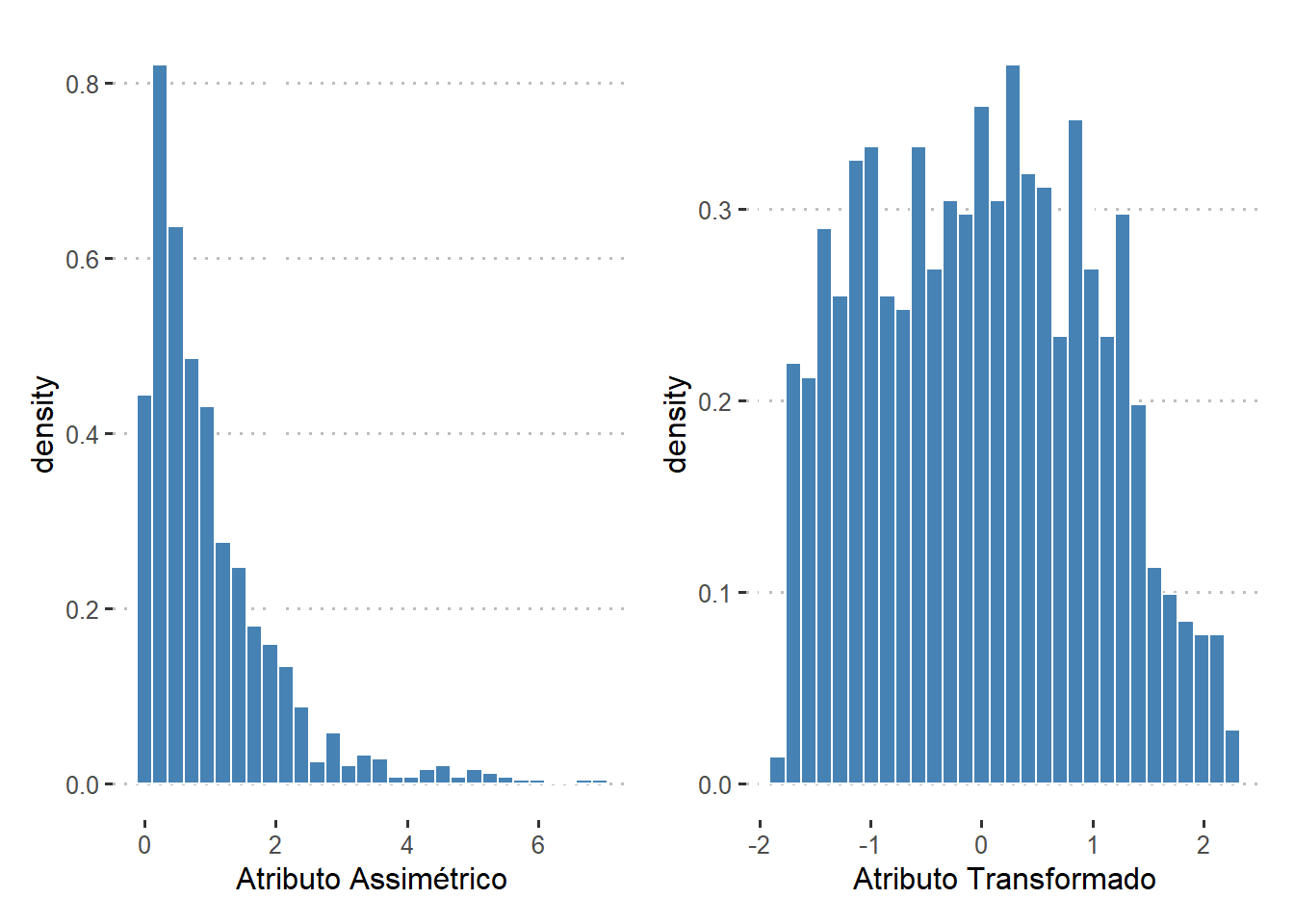
A transformação Yeo-Johnson é definida pela seguinte equação:

$$ y = \begin{cases} \dfrac{(x + 1)^\lambda - 1}{\lambda}, & se \ x \geq 0, \ \lambda \neq 0 \\ \ln(x + 1), & se \ x \geq 0 \ \lambda = 0 \\ \dfrac{-((-x + 1)^{(2 - \lambda)} - 1)}{(2 - \lambda)}, & se \ x < 0, \ \lambda \neq 2 \\ -\ln(-x+1) & se \ x < 0, \ \lambda = 2 \end{cases} $$

onde $x$ é a variável a ser transformada e $y$ é a variável transformada.

Em resumo…

Transformar variáveis é útil para melhorar a qualidade da modelagem e a precisão das previsões em modelos preditivos. As transformações são aplicadas às variáveis independentes para melhorar a distribuição, escala e relação com a variável de saída. Existem várias técnicas de transformação disponíveis, incluindo transformação logarítmica, transformação de raiz quadrada, transformação de Box-Cox e a transformação de Yeo-Johnson.

Não há uma única transformação de variáveis que seja a melhor para todos os casos. É importante lembrar que a escolha da transformação deve ser baseada em uma avaliação cuidadosa da natureza dos dados e da relação entre as variáveis. A transformação escolhida deve ajudar a reduzir a heterogeneidade de variância e normalizar a distribuição dos dados, mas também deve ser interpretável e fazer sentido do ponto de vista teórico.

Até breve! 👋